最高のコレクション 三角形 内角 求め 方 163206

 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか まとめ：直角三角形の比3つを使い倒せ！ 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのはθ = b c , tan ⁡ θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算

内接円 内心

三角形 内角 求め 方

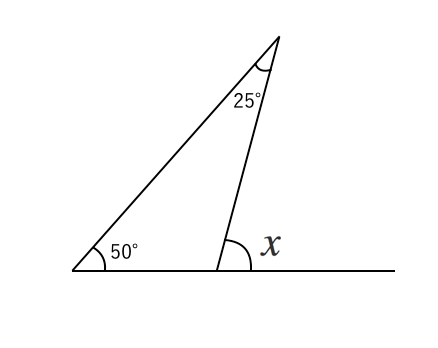
三角形 内角 求め 方-三角形の外角の求め方 ① 外角 = 離れた2つの内角の和 ex) c の外角＝ab ② 外角 = 一直線 （ いっちょくせん ） 180° その内角( ←当然) ex) c の外角＝180°c (当然と言えば当然ですね。 三角形の 内角の和 は180°、 一直線 も180°、180°つながりですね！) 多角形の内角の求め方が分かりません。 『このような計算式をつかい、こう計算すれば多角形の内角の和が求められる』っていう風に覚えるしかないので、深く考えないほうがいいですよ。 n角形の内角の和はこれらの三角形の内角の総和に等しいの

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

 多角形の内角の和の公式 三角形の内角の和： 180° 180 ° 四角形の内角の和： 360° 360 ° 五角形の内角の和： 540° 540 ° 六角形の内角の和： 7° 7 ° ・・・ n角形の内角の和： 180°× （n−2） 180 ° × （ n − 2 ） この公式は覚えやすいので暗記してもいい 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m三角形の内角の性質 三角形の内側にある角のことを 内角 といい、 すべて足すと180° になります。 これは小学生のときに学習しているので覚えている方も多いでしょう。 でも じゃぁ、何で180°になるのか知っていますか？ と言ったら、困ってしまい

 正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる！ 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、正しい値が出てきません。「三角形の3辺の長さから3角の角度を計算します。」変数の値がa=10b=100c=100の時、「高さ h」の答えが間違っている。正解は keisanより 高さhの計算を修正しました。ご指摘ありがとうございました。 0540紙に書いた三角形を切って確認することですが ここではもう少し論理的に確認していこうと思います。 上の図は適当に書きましたので、 私にもそれぞれの角度がどれくらいか分かりません。 でも、内角の和は求められます。

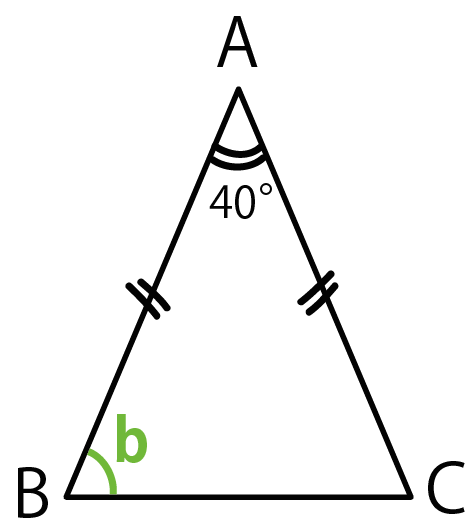
頂角の求め方、二等辺三角形との関係 頂角の求め方を下式に示します。 頂角＝180°－2×底角 三角形の内角の和は180°です。2つの底角の角度は等しいので180°から底角の2倍を引いた値が頂角となります。 下図の二等辺三角形の頂角を求めてください。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2＝360°になります。 ですのでaの角度は、360°(72°38°30°)＝2° よって、 答え a＝2 ° 角度③ 応用問題 例題4 1組の三角定規を下の図のように重ねました。この図でaの角度は何度になるか求め 多角形の内角の和の求め方 角形の内角の和は次のように求めれます。 例 十角形 ⇒ 十二角形 ⇒ なぜ上のような式で求めることができるのか確認しておきましょう。 三角形の内角の和が180°になるというのは知っての通りだね。 これを利用すると

三角形の角度を求める 思考力を鍛える数学

三角形の辺から角度を計算 製品設計知識

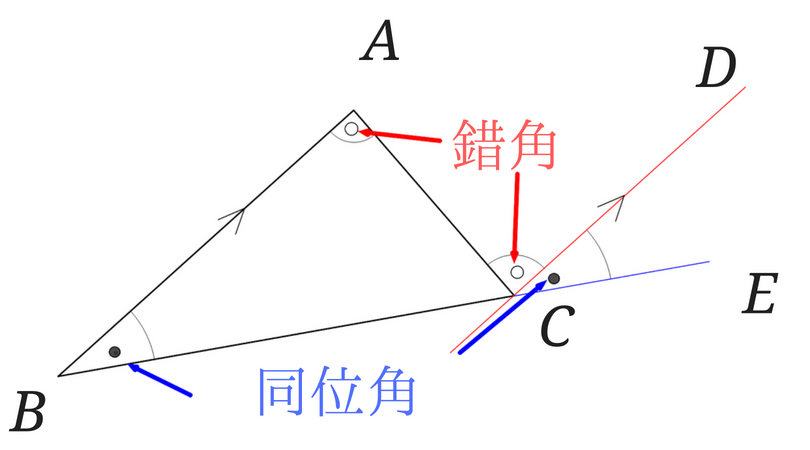
 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ＝となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 直角三角形とは、三角形の つの内角のうち、 つの角が直角である三角形 です。 また、直角に向かい合う辺のことを「 斜辺 」といいます。 補足 なお、小・中学校で習う「直角三角形の書き方」については以下の記事で説明しています。 正三角形・二 この記事では、三角関数について、角度の求め方や変換公式（\\(90^\\circ − \\theta\\) など）について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね！

人気ダウンロード 三角形 内角 求め方 シモネタ

三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局

 見極め方ポイント ステップ1：内角に直角がある → Yes ： 直角三角形 No ：ステップ2へ ステップ2：内角の1つが 鈍角 だ → Yes ： 鈍角三角形 、 No ： 鋭角三角形 よし、次！ 三角形の後は、四角形、五角形・・・多角形について！ 中2数学：多角形の内角三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。正多角形の内角・外角の求め方を解説！←今回の記事 星形の角度の求め方を解説！ ブーメラン型の角度の求め方！ ちょうちょ型の角度の求め方を解説！ 合同な図形の基本性質とは？ 三角形の合同条件を使って、合同な三角形を見つける方法！

ファイル 三角形の内角と外角 Png Wikipedia

直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo

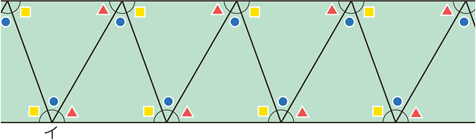
 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは，三角形の内側の角の大きさの和のことをいいます。 三角形の内角の和＝180° 小学生女の子 正三角形の1つの角の大きさが60°で角は3つだから三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。

三角形の角度を求める問題 小学生 中学生の勉強

内角の和 算数用語集

内接円 内心

三角形の角度を求める問題 小学生 中学生の勉強

余弦定理で角度を求める方法 数学の星

三角形の３辺から角度を計算 高精度計算サイト

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

なぜ三角形の内角の和は180度 Qiita

直角三角形の解法 1

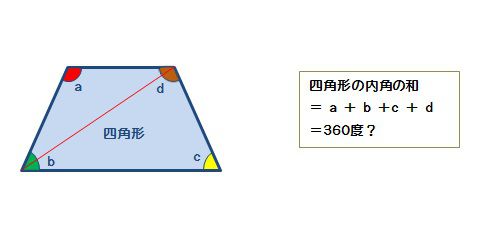
四角形の内角の和 算数の公式覚えてますか

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形の内角と外角の性質 教遊者

角度の計算 裏技まとめ 教遊者

Math 平行と合同 角の二等分線と角度 働きアリ

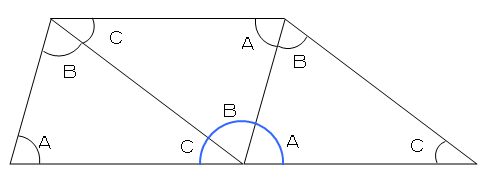
三角形の内角と外角の関係

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

立派な 三角形 の 内角 の 求め 方 壁紙 おしゃれ トイレ

三角形の内角の和 内角を全部足すと１８０ になる公式 中学や高校の数学の計算問題

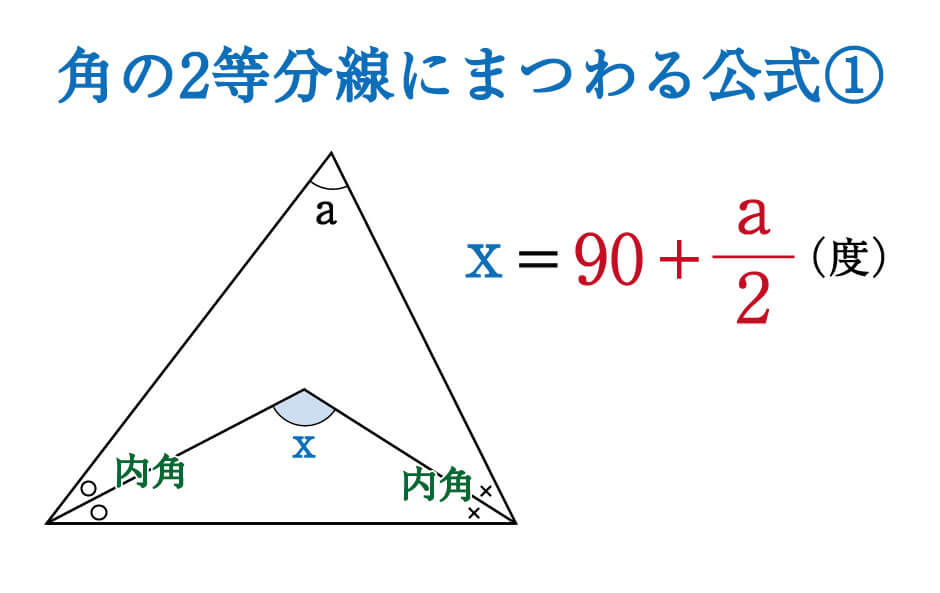
数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月

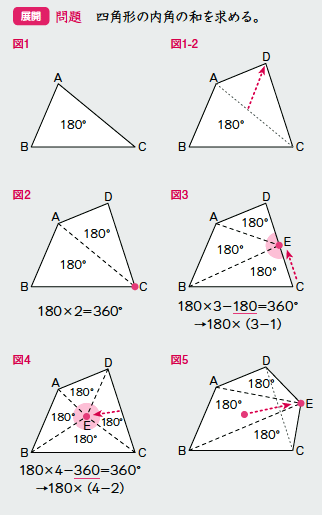
活用 の視点を取り入れた授業例 ２ 図形の性質 四角形の内角の和 ５年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所

正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典

三角形の内角の和 算数の公式覚えてますか

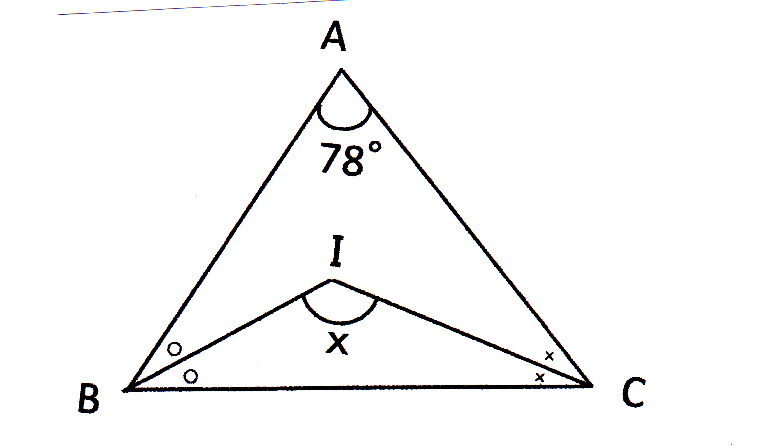
三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方

3

直角三角形の解法 1

5年 三角形のふしぎ 算数イメージ動画集 大日本図書

三角形の内角の和は本当に180 か 数学って面白い

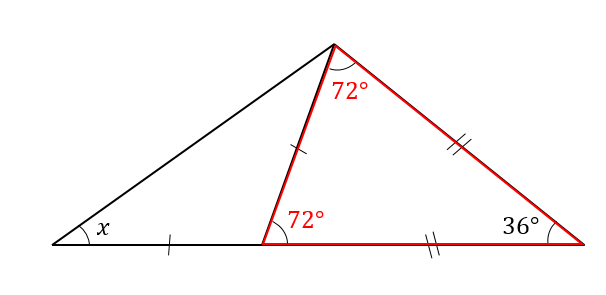
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ

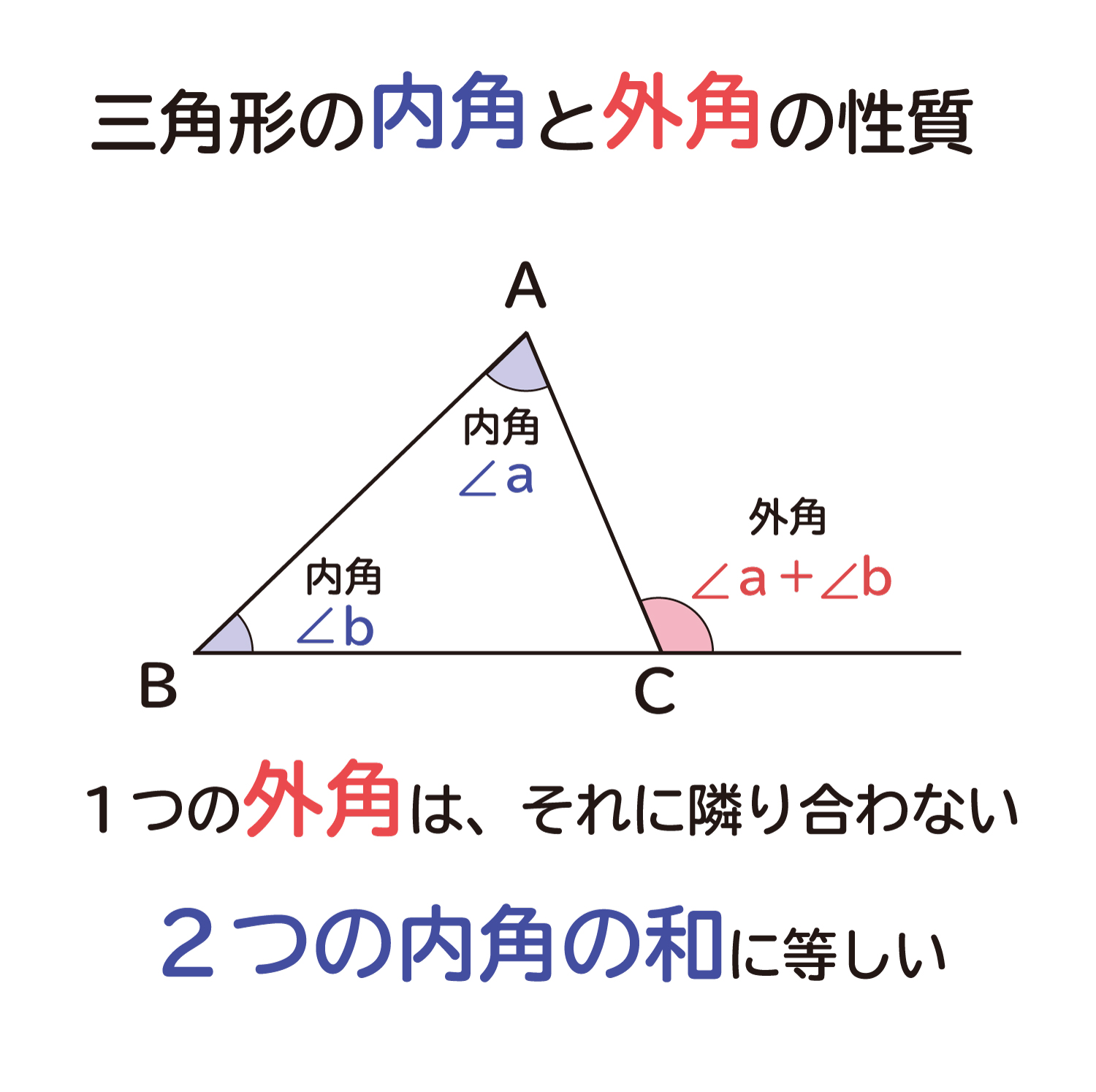
なぜ 三角形の１つの外角は それと隣り合わない２つの内角の和に等しい のか を説明します おかわりドリル

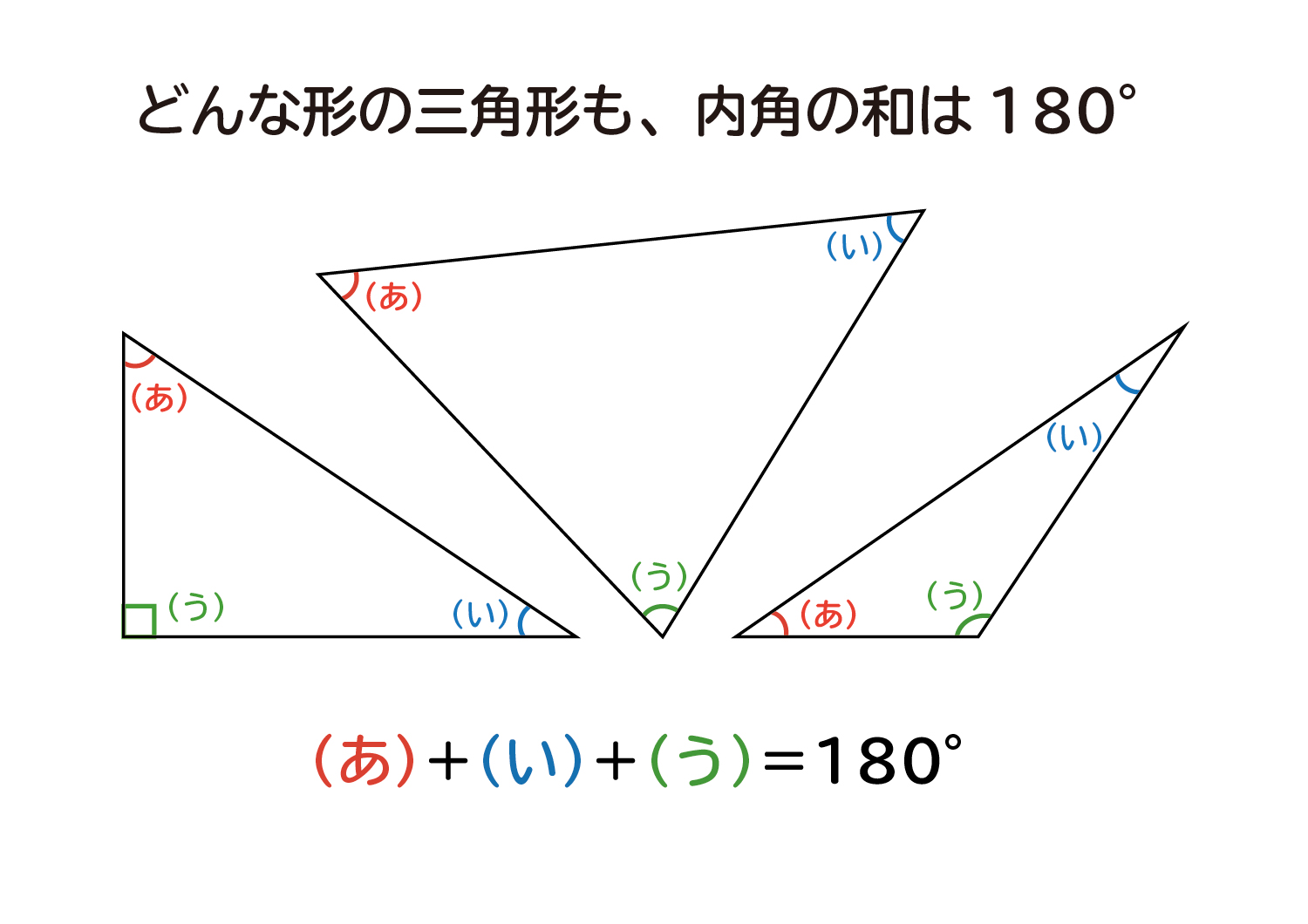
なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル

三角形の内角の和 Jsciencer

中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形の内角と外角の関係 個別学習塾ナレッジ

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

1

あ かまでの角度を求めてください 急いでます 教えてください Clearnote

中2数学 複雑な多角形 角の和 応用問題

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

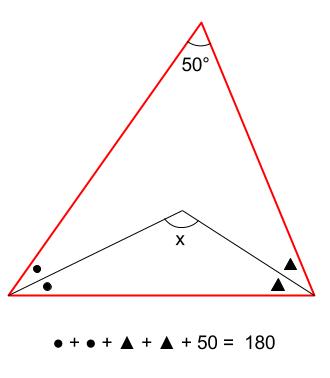
中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su

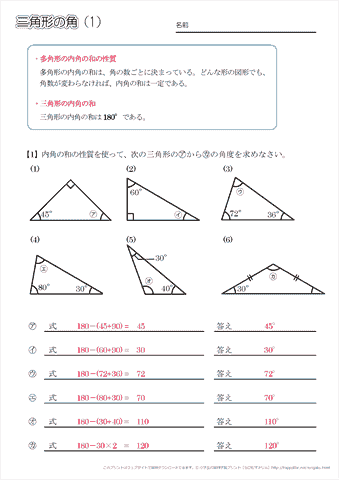
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

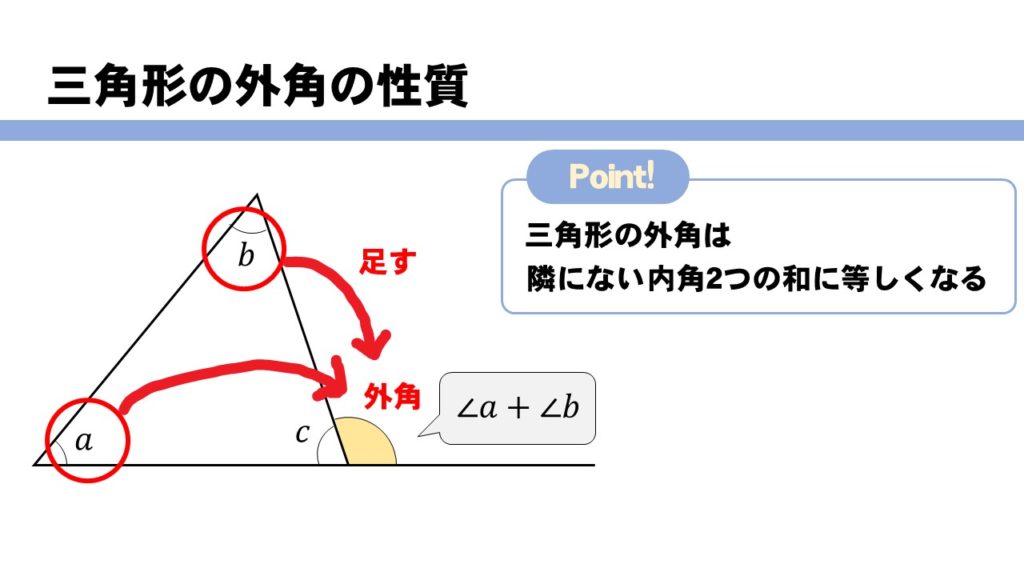
3分なるほど 三角形の内角 外角の性質について解説 数スタ

正三角形や二等辺三角形の内角 Youtube

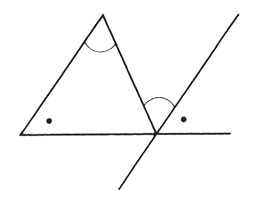
内角の和 算数用語集

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

内角の和 算数用語集

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

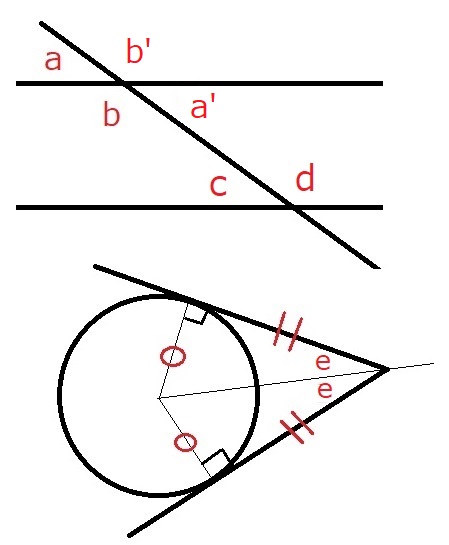
三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

小５ 算数 小５ ３１ 三角形の角 Youtube

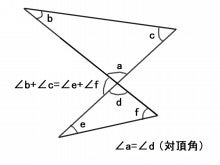
角度の求め方 数学が嫌いなんです

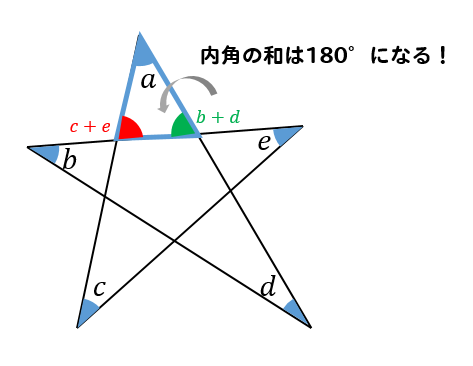
星形の角度 内角の和の求め方を問題解説 数スタ

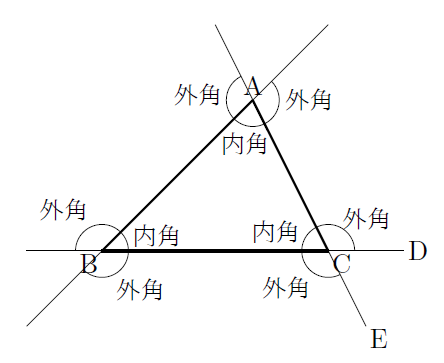
三角形の内角と外角 まなびの学園

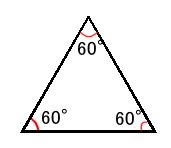
正三角形の内角の和

角度の求め方 算数の教え上手 学びの場 Com

数学 中2 48 三角形の内角と外角 基本編 Youtube

三角形の内角の和

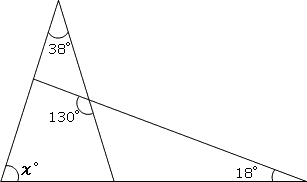
角度の求め方 算数の教え上手 学びの場 Com

内接円 内心

中学数学 内角と外角の関係を利用した問題 実は公式不要 なぜか分かる はかせちゃんの怪しい研究室

タンジェントとは何か 中学生でも分かる三角関数の基礎

円と三角形 角度 中学から数学だいすき

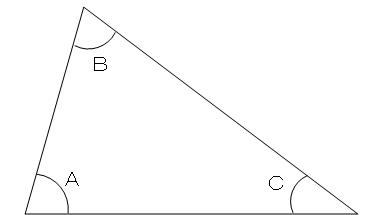
三角形の内角と外角の関係

角度の求め方 算数の教え上手 学びの場 Com

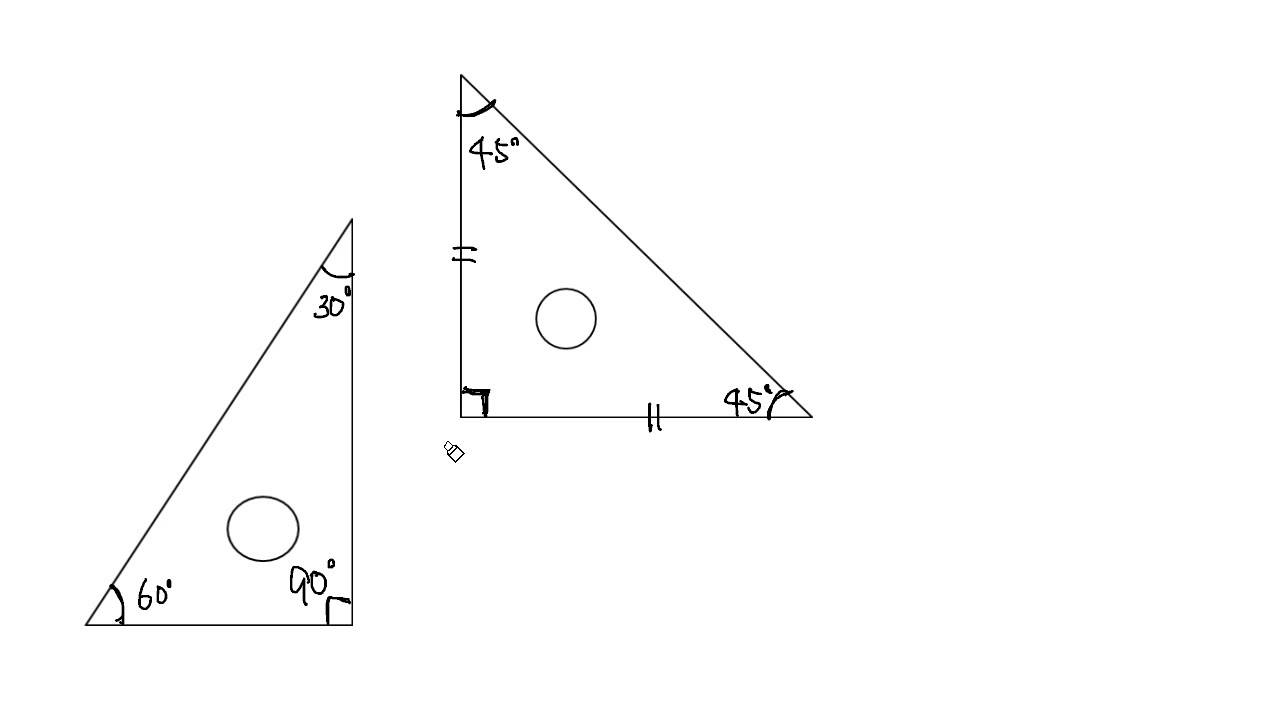
三角形の内角の和 Youtube

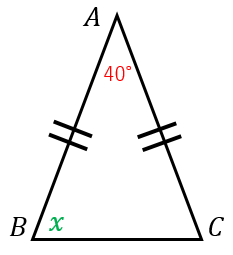
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

3

図形の扉 三角形の外角の定理

内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学

三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

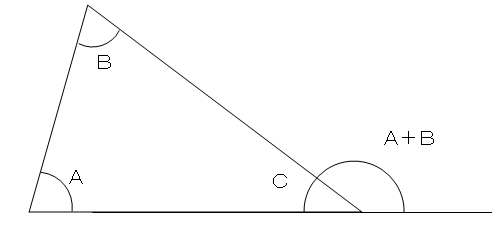
三角形の内角と外角の関係

三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

1

底辺と高さから角度と斜辺を計算 高精度計算サイト

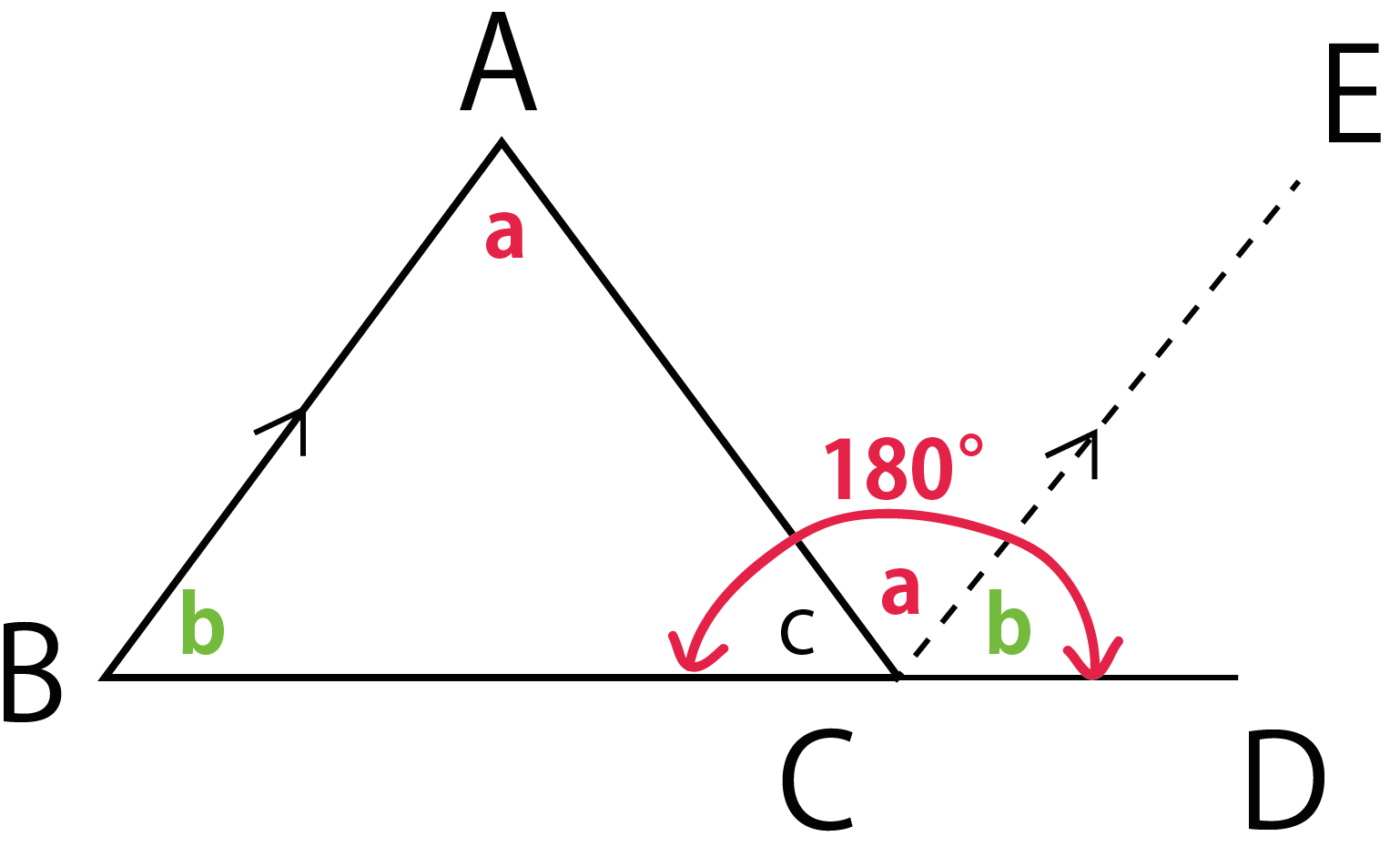
中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

70以上三角形内角外角 シモネタ

数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

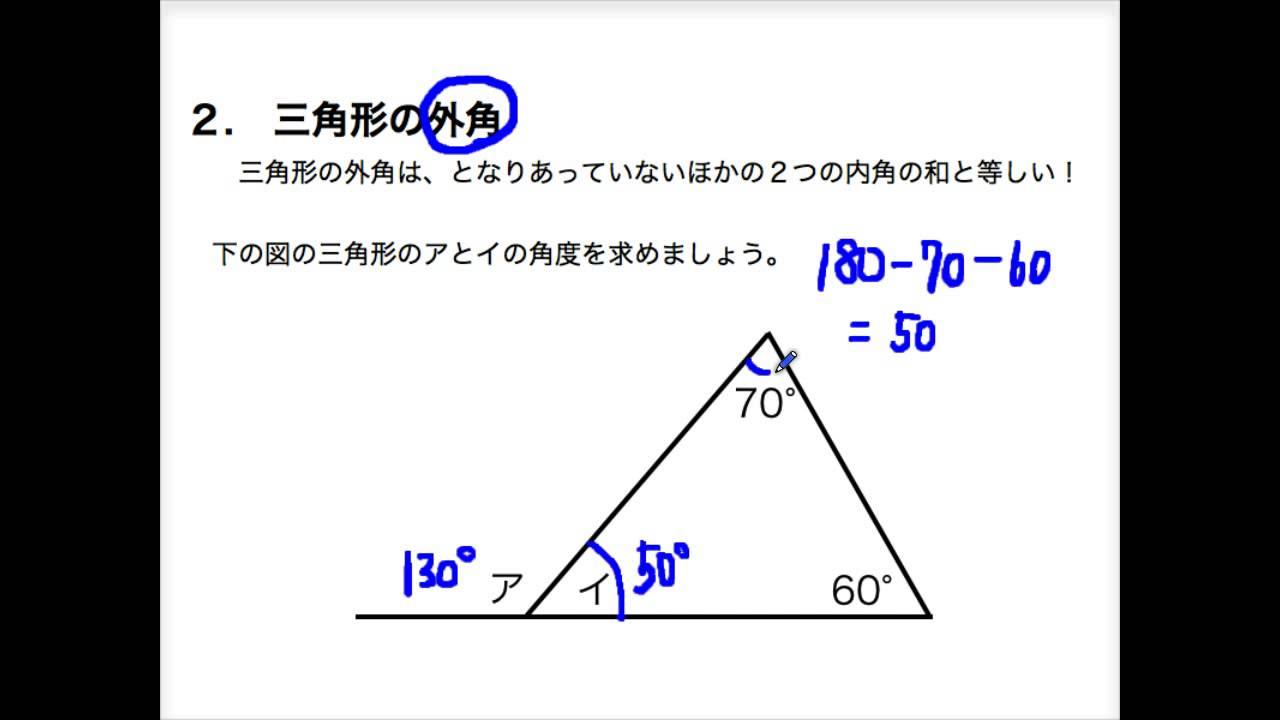
小学校5年 算数 三角形の外角 Youtube

角度の問題まとめ 無料で使える中学学習プリント

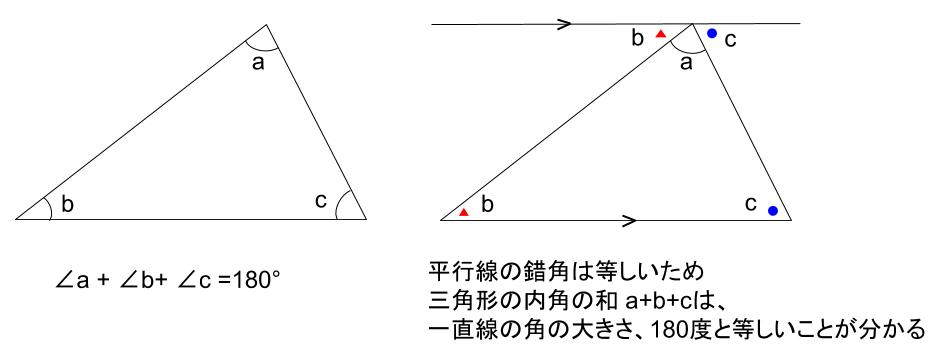
中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su

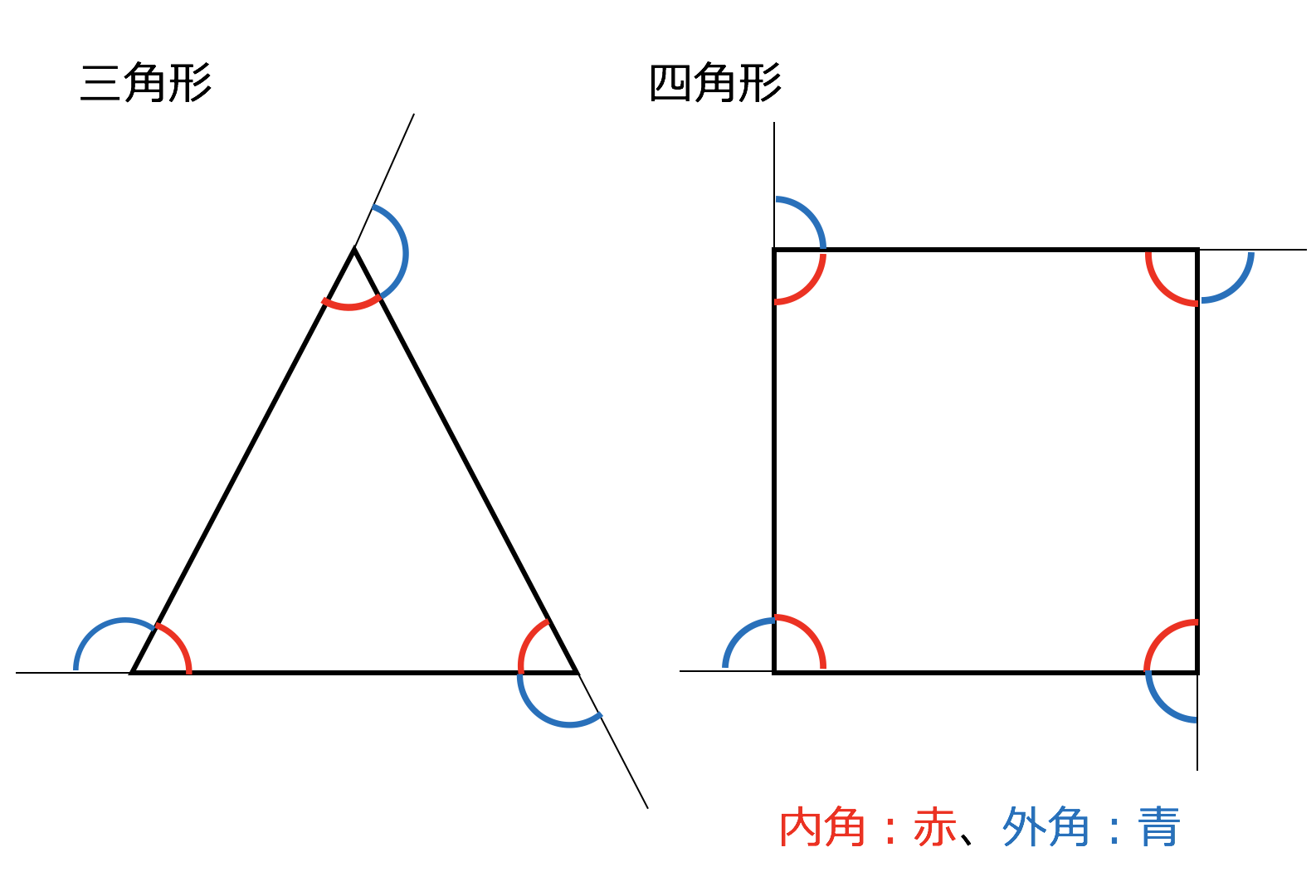
3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ

二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明

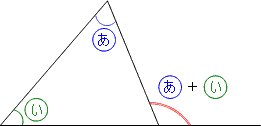
角度の求め方 算数の教え上手 学びの場 Com

多角形の内角の和 外角の和の公式 数学fun

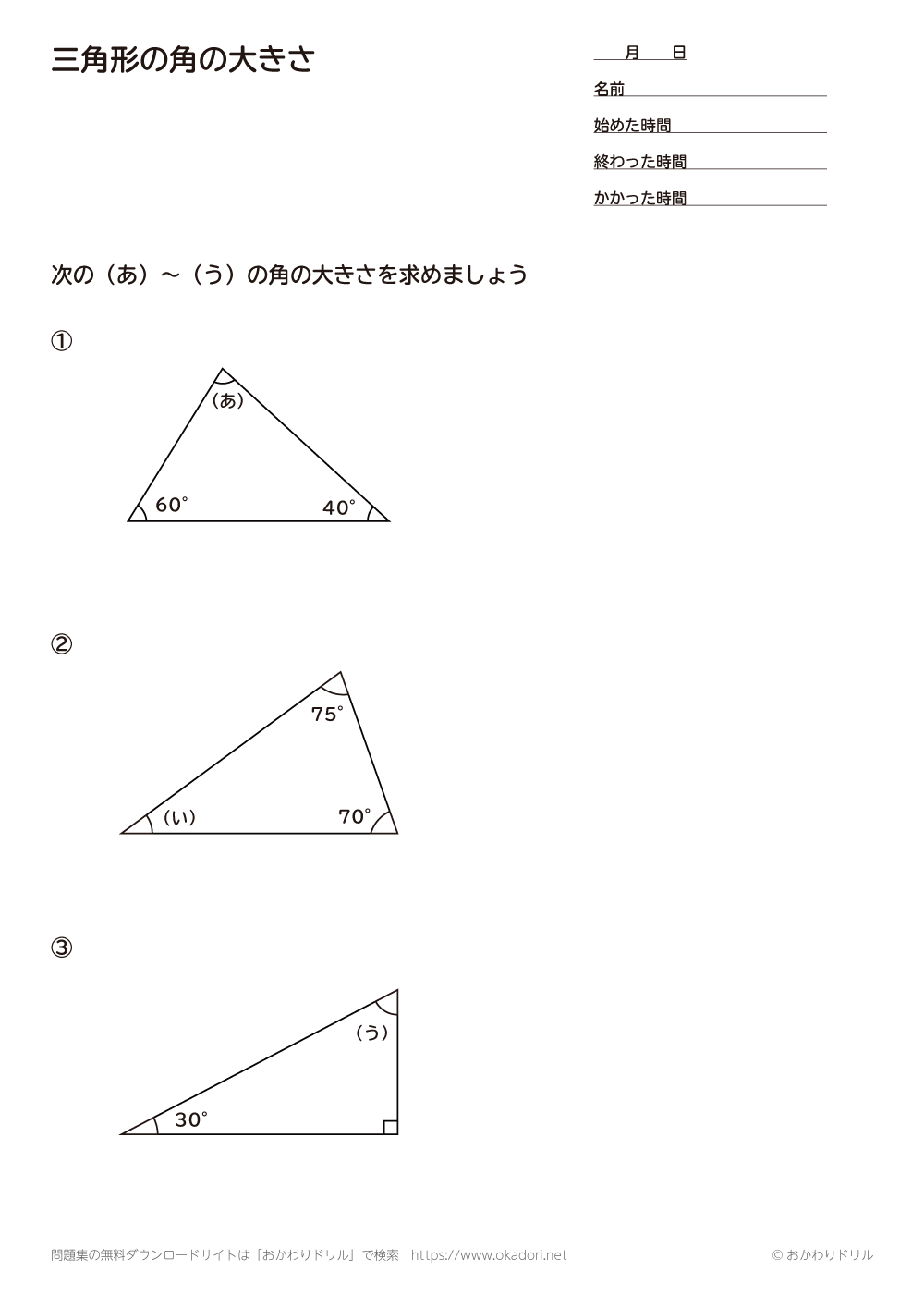
小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

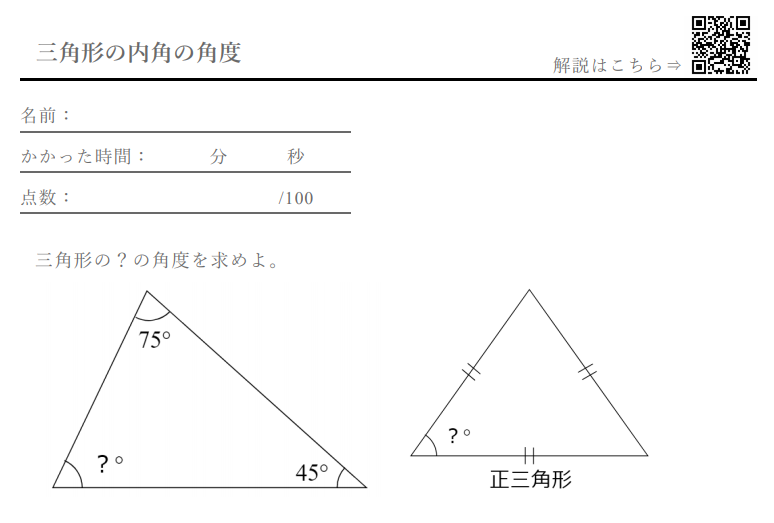
三角形 の内角の角度 計算ドリル 問題集 数学fun

二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思う Clearnote

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す